增量式PID计算公式解析

一开始见到PID计算公式时总会问“为什么是这样子的一道公式”，为了理解那几道公式，当时将其未简化前的公式活生生地算了一遍，现在想来，这样的演算过程固然有助于理解，但假如一开始就带着对疑问的答案已有一定抽象了解后再进行演算则会理解的更快！

首先推荐白志刚的《由入门到精通—吃透PID 2.0版》看完一、二章之后，建议你先通过实践练习然后再去看书里接下来的其他章节，这样你对这本书的掌握会更加高效。

PID就是对输入偏差进行比例积分微分运算，然后将运算的叠加结果去控制执行机构。实践练习中，如何把这一原理转化为程序？为什么是用那几个error进行计算?

以下是我摘录的一段PID程序，我曾用其对智能车的速度进行闭环控制：

P：Proportional 比例

I：Integrating 积分

D：Differentiation 微分

Pwm_value：输出Pwm暂空比的值

Current_error：当前偏差

last_error：上次偏差

prev_error：上上次偏差

增量式PID计算公式：

P=Kp*(current_error﹣last_error)；

D=Kd*(current_error﹣2*last_error﹢prev_error)；

I=Ki*current_error；

PID_add=Pwm_value+P﹢I﹢D；

一、为什么是PID_add=Pwm_value+（P﹢I﹢D）而不是PID_add=P+I+D？

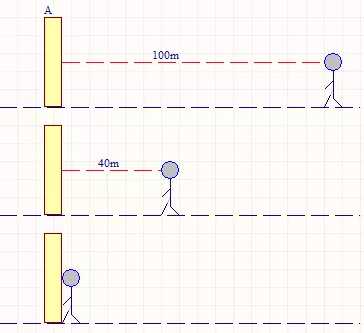
如上图，有一个人前往目的地A，他用眼睛视觉传感器目测到距离目的地还有100m，即当前与目的地的偏差为100，他向双脚输出Δ=100J的能量，跑呀跑，10s之后，他又目测了一次，此时距离为40m，即current_error=40，他与10s前的偏差last_error=10对比，即current_error - last_error=-60，这是个负数，他意识到自己已经比较接近目的地，可以不用跑那么快，于是输出Δ=100+(-60)=40J的能量，40J的能量他刚好以4m/s的速度跑呀跑，10s之后，他发现已经到达目的点，此时current_error=0，大脑经过思考得出current_error—last_error=0 - 40=-40，两脚获得的能量Δ=40+(-40)=0，即他已经达到目的地，无需再跑。在刚才的叙述中，可知增量式P+I+D输出的是一个增量，将该增量与调节量相加后所得到值才是最终输出量，其反应的是之前的输出量是在当前的状态中是该增加还是该减少。

二、纯比例控制P=Kp*(current_error﹣last_error)，怎样理解﹙current_error﹣last_error ﹚？

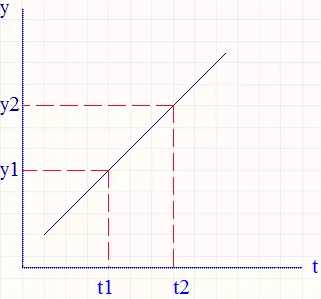
比例表示变化趋势，微分则表示变化趋势的变化率，映射到一个图像曲线中即为导数的变化！上图中若求曲线中x2至x1某点的斜率，当Δt足够小时，则可近似为(y2 - y1)／Δt ，可知x3到x1导数的变化为﹛(y3 - y2) -(y2 - y1)﹜／Δt ＝(y3 - 2*y2﹢y1)／Δt 。将不同时间的y1、y2、y3映射为prev_error、last_error、current_error；则error变化趋势的变化为﹛(current_error - last_error) - (last_error - prev_error)﹜／Δt=﹛﹙current_error - 2*last_error﹢prev_error﹚﹜／Δt，可得微分D=Kd*(current_error﹣2*last_error﹢prev_error)。在系统中加入微分反映系统偏差信号的变化率，能预知偏差变化的趋势，具有超前控制作用，提前处理偏差。

四、引进积分控制？

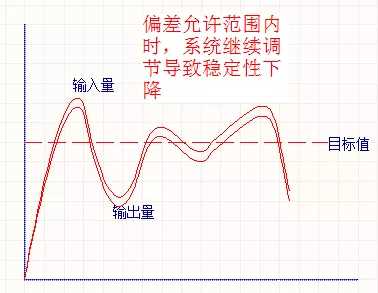
积分控制可以消除偏差，体现在公式中较容易理解，当前的偏差差经过系数Ki的放大后映射为输出控制量，即I=Ki*current_error。P只要前后偏差之差为0，即current_error - last_current=0，则不进行调节，D只要前后偏差变化率为0，即(current_error﹣2*last_error﹢prev_error)=0，则不进行调节。而对于积分只要偏差存在，调节就始终进行，因此积分可以消除误差度，但在在某些情况下，一定范围内的误差是允许的，而如果此时积分调节始终存在，可能会导致系统稳定性下降，如上图，此时可通过弱化积分系数Ki使系统稳定。